This paper got published in July already, but I had not had the time yet to blog about this exciting work by
Irini Furxhi and Ammar Ammar:
A data reusability assessment in the nanosafety domain based on the NSDRA framework followed by an exploratory
quantitative structure activity relationships (QSAR) modeling targeting cellular viability
(doi:10.1016/j.impact.2023.100475)
The study has two sides to it: first, it looks into how far we are with QSAR
in the field of nanosafety. We have limited data, but this paper got together 34 data sets, and in the model building
many different possible factors are explored. Now, as a scholar, I would really want to know which factors are
really important. We have been studying this for some time, e.g. in the past RRegrs paper
(doi:10.1186/S13321-015-0094-2). Basically, I think we still
don’t really understand the relation between the data characteristics and the modelling options. When is
data rich enough to move from classification to regression? How much (many) exerimental data do we need,
for the model to capture a certain applicability domain sufficiently?
Actually, I think the rise of deep learning approaches shows us a few things: more data actually does help.
But also, with enough data, the representation becomes less important for the overall pattern. There are
even hints that deep learning needs a certain level of noise. Did anyone study that phenomenon yet?
Now, the reader of this paper will not be disappointed. The design is complex and there are many small hints
about what worked and what did not. But this gets us to the other side of this story.
The second side of this paper is the question whether the level of FAIR-ness helps this QSAR modelling.
Earlier, Ammar studied the R1.3 aspects of nanosafety research. The R1.3 guiding principle expects that
(Meta)data meet domain-relevant community standards.
Ammar’s research (preprint doi:10.26434/CHEMRXIV-2022-L8VK8-V2)
shows we can link this to actual reuse, where QSAR is one of those use cases.
In their July paper, they show how we can integrate the use of the community standards
in a reproducible way to support nanosafety research.
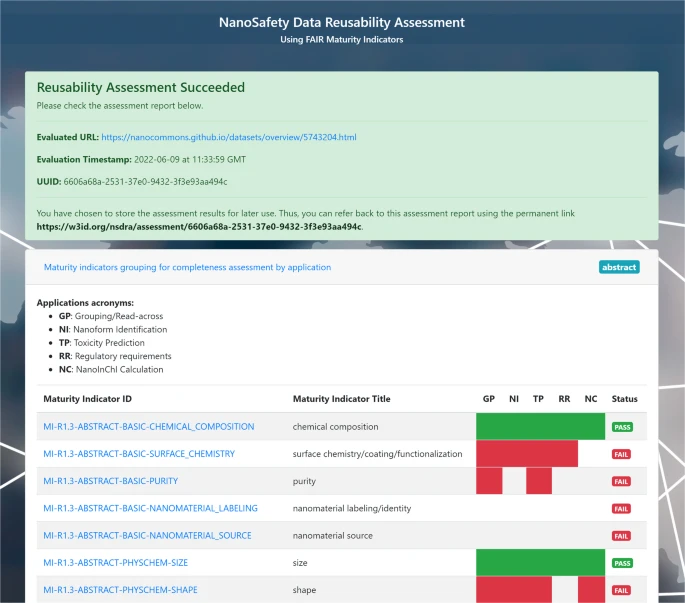
The following screenshot from the article (Figure 2, CC-BY) shows the relation between R1.3 maturity
indicators and QSAR variables:
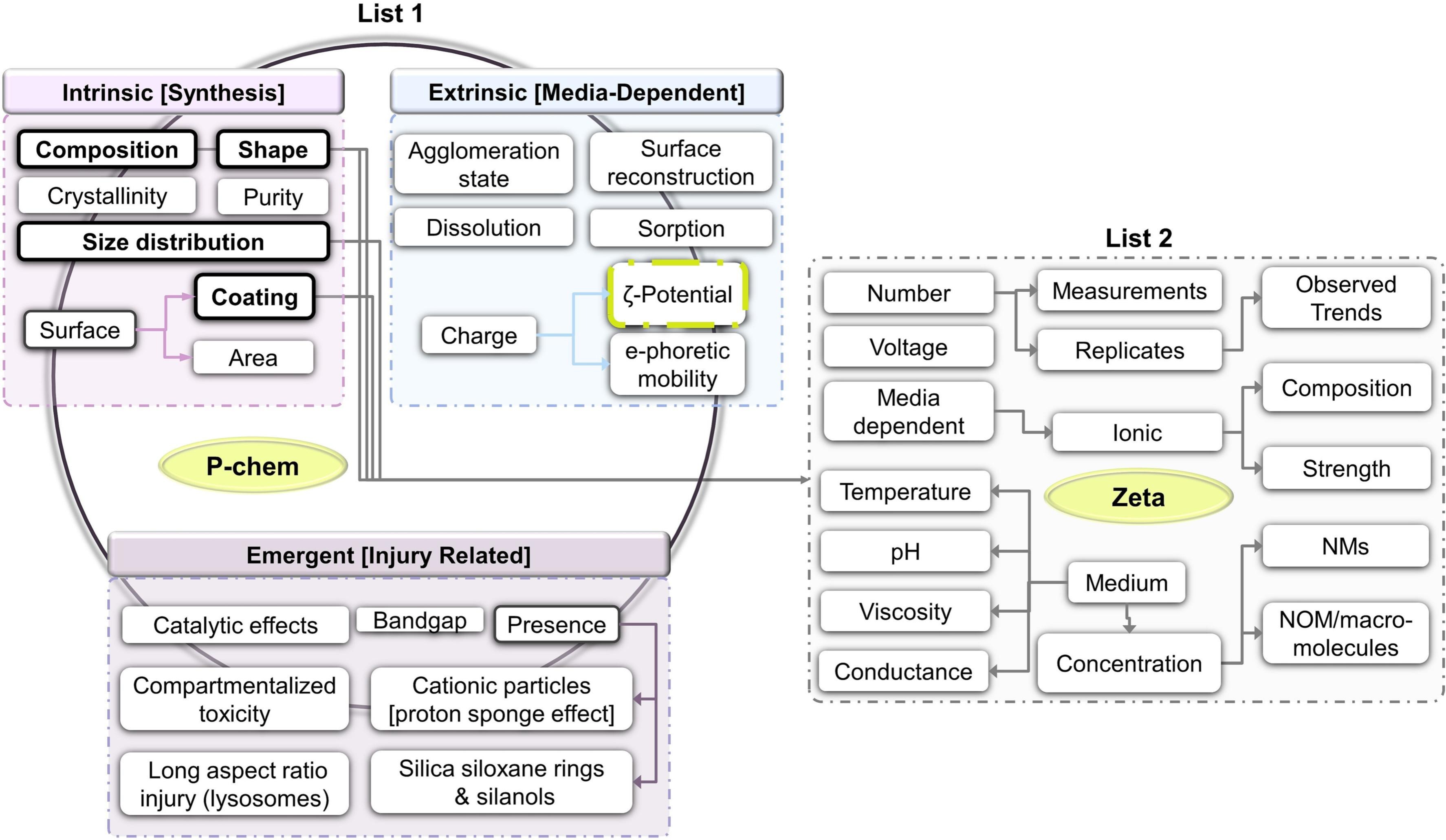
I think Furxhi and Ammar may actually have introduced a new community standard: this is how nanoQSAR
research should be done from now on. Irini and Ammar, thanks for this great collaboration!
]]>